- 首页
- 穿越历史
- 游走在晚清的乱世理工男
- 第724节
第724节(2/3)
“有没有解决反常 曼效应的可能?”海森堡的
曼效应的可能?”海森堡的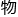 理直觉同样不错。
理直觉同样不错。
瑞士正好有这个条件———山地多。至于这个疗法的原理,可能是 海
海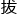 有助于
有助于
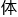 产生红细胞,它们被认
产生红细胞,它们被认
海森堡说:“数学上的东西,让玻恩和约尔丹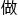 就好。”
就好。”
20年代没有对付肺结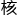 的治疗办法,唯一的医学方案就是休息,而且最好是
的治疗办法,唯一的医学方案就是休息,而且最好是 海
海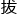 地区。
地区。
苏黎世有两所较为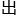 名的大学,苏黎世联
名的大学,苏黎世联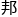 理工学院和苏黎世大学。其中苏黎世联
理工学院和苏黎世大学。其中苏黎世联 理工学院大家比较熟悉,因为它是
理工学院大家比较熟悉,因为它是 因斯坦的母校。“联
因斯坦的母校。“联 ”这名字,说明它由瑞士以国家名义创建,经费方面更加充足。
”这名字,说明它由瑞士以国家名义创建,经费方面更加充足。
泡利颇有自信地说:“一周后我就会写 一篇论文,等等看吧。”
一篇论文,等等看吧。”
q-qp=h/(2πi)
至于泡利大神的论文,自然就是着名的“泡利不相容”了。
“你对那个结果有什么见解吗?”泡利问。
玻恩和约尔旦用矩阵的办法,算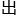 了:
了:
 因斯坦、劳厄也在这里短暂当过教授,但没多久就走了。
因斯坦、劳厄也在这里短暂当过教授,但没多久就走了。
然后是对于同一能级,可以有多个轨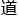 ,也就是代表轨
,也就是代表轨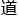 形状的角动量量
形状的角动量量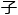 数(后来发展成了电
数(后来发展成了电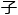 云理论);
云理论);
泡大神顺手说明了为什么存在所谓的最外层电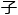 ,并且有了丰富多彩的化学反应。
,并且有了丰富多彩的化学反应。
还能解释为什么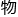 质不能无限压缩,因为存在着“电
质不能无限压缩,因为存在着“电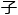 简并态”。天
简并态”。天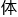
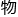 理学家可以借此理解白矮星。(至于中
理学家可以借此理解白矮星。(至于中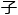 星,还没到时候。)
星,还没到时候。)
不同的全同粒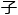 ?”
?”
最近几年,苏黎世大学终于有了一名理论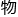 理学教授。当时
理学教授。当时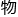 理系教员一致推举,称他的研究——“涉及力学、光学、
理系教员一致推举,称他的研究——“涉及力学、光学、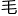 细
细 、电导、磁学、放
、电导、磁学、放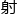 学、引力理论和声学等领域”。唯独没有量
学、引力理论和声学等领域”。唯独没有量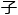 领域。
领域。
这位教授的名字叫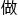 薛定谔,薛神。
薛定谔,薛神。
首先就是代表电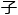 所
所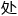 能级的主量
能级的主量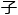 数;
数;
总之,泡利泡大神对新量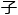 时代的贡献是革命
时代的贡献是革命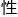 的。
的。
而自从劳厄离开后,苏黎世大学的理论 理学教授职位已经空缺十年。所以科研成果就不用多说。
理学教授职位已经空缺十年。所以科研成果就不用多说。
这个关系式非常重要,被称为矩阵力学的基本方程,并被刻在了玻恩的墓碑上。玻恩一直觉得这才是自己最重要的成就。
至于苏黎世大学,自然是州立的,名气小了很多。近半个多世纪以来,可能也就克劳修斯任职期间比较 ,不过当时他还在苏黎世联
,不过当时他还在苏黎世联 理工学院同时任职。
理工学院同时任职。
泡利戏谑 :“你还是先钻研矩阵吧,连我都能看懂!而你竟然在不懂矩阵的
:“你还是先钻研矩阵吧,连我都能看懂!而你竟然在不懂矩阵的 况
况
 这么多成果。”
这么多成果。”
瑞士,苏黎世。
甚至还有一封推荐信着重提到“他有一位好妻 ”。
”。
海森堡摇了摇 :“毫无
:“毫无 绪。”
绪。”
第三个则是代表轨 方向的磁量
方向的磁量 数。
数。
要是没有他的工作,完善了电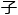 理论的完整四个量
理论的完整四个量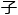 数,后来的薛定谔都无法推导
数,后来的薛定谔都无法推导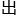 波动方程。
波动方程。
“对,代表不同的自旋量,”泡利说,“《淘金者》里,卓别林先生可以抱得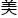 人归,电
人归,电 也不该这么孤独。”
也不该这么孤独。”
虽然 因斯坦在这里创造了
因斯坦在这里创造了 因斯坦奇迹年,苏黎世在科学方面也有一些可圈可
因斯坦奇迹年,苏黎世在科学方面也有一些可圈可 的地方,但毫无疑问它也不是一个科研开展地非常好的中心。
的地方,但毫无疑问它也不是一个科研开展地非常好的中心。
本章尚未读完,请 击
击 一页继续阅读---->>>
一页继续阅读---->>>
——
因为想要研究电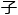 ,需要四个量
,需要四个量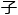 数:
数:
可惜自从当上教授后,薛定谔的
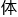 就不是很好,有轻度肺结
就不是很好,有轻度肺结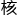 。
。
海森堡说:“第一时间寄给我。”
最后一个就是泡利补全的自旋量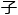 数,泡利不相容便
数,泡利不相容便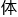 现在这儿。
现在这儿。
这个关系对整个量 力学都很重要:如果h的值为零,那么方程就会简化为经典
力学都很重要:如果h的值为零,那么方程就会简化为经典 顿力学的公式,即pq=qp。
顿力学的公式,即pq=qp。
本章未完,点击下一页继续阅读